建築における梁(はり)とは、建物の構造を支える非常に重要な部材の一つです。簡単に言うと、水平方向に架けられる部材のことで、主に上からの重さ(荷重)を受け止めて、それを柱や壁に伝える役割を果たします。
梁の役割
梁の主な役割は以下の通りです。
- 垂直方向の荷重を支える: 屋根や床、その上の階の床や家具、人などの重さ(鉛直荷重)を支えます。これらの荷重は梁に集められ、さらに柱や壁へと伝えられ、最終的に基礎を通して地面へと流されます。
- 水平方向の力に抵抗する: 地震や台風などの際に建物にかかる横からの力(水平力)に抵抗し、建物の変形や倒壊を防ぎます。柱と梁が一体となって働くことで、建物の剛性が高まり、耐震性や耐風性が向上します。
- 柱を固定する: 柱と柱の間を梁でつなぐことで、柱が安定し、横方向への倒れを防ぐ役割もあります。
梁のモーメント
- 矩形断面の梁(高さH)が曲げモーメントを受けるとき、曲げ応力だ最大となるのは
梁の上面又は下面である - 矩形断面の梁(高さH)が曲げモーメントを受けるとき、せん断応力が最大となるのは
梁高さの中央面である - 断面二次モーメントは、「材料の曲げにくさ(曲げる力に対する抵抗性)」を表します。断面二次モーメントが大きいほど、曲げにくい材料を示す
- 矩形断面の梁の幅を一定として、高さHを2倍にすると、せん断二次モーメントは
8倍(3乗)になる - 片持ち梁の自由端に集中荷重が作用するとき、梁高さが2倍になると、梁に生じる最大曲げ応力は
1/4倍になる
考察例
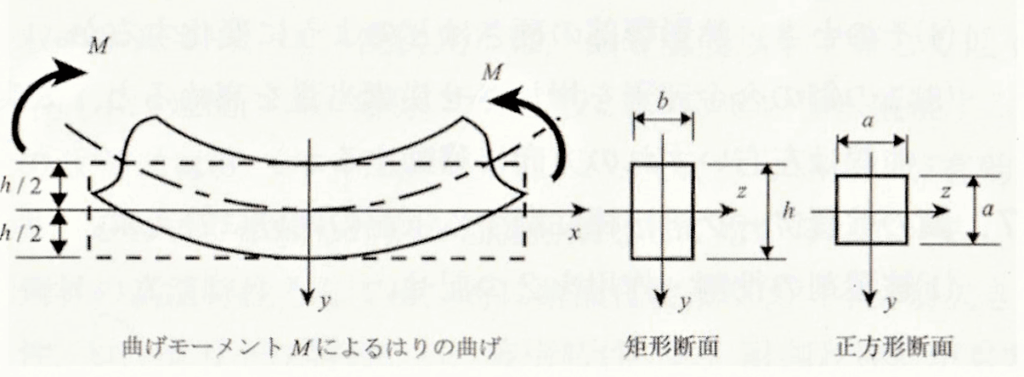
下図のような断面積が同じ、矩形断面はり(幅b、高さh)と正方形断面はり(幅a、高さa)がある。両はりが同じ大きさの曲げモーメントMを受けるとき、矩形断面はりの最大曲げ応力を正方形断面はりの1/2にするには、 矩形断面はりの寸法をどのように設定すればよいか、下記の手順に従って求めよ。なお、矩形断面はりの断面二次モーメントIは、I=bh³/12で与えられる
回答手順
- ①はりの曲げ応力σは、中立軸からの距離をyとすると、σ=M×y/I(断面二次モーメント) で求められる。
- ②したがって、矩形断面はりの最大曲げ応力σmaxは、σmax=M×2/h/I となり、σmax=M×12/bh³×h/2となる
- ③一方、正方形断面はりの最大曲げ応力σmaxは、②においてb=h=aとおけばよいので、σmax=M×12/a⁴×a/2となる
- ④「矩形断面はりと正方形断面の断面積が同じ(bh=a²)」と「矩形断面はりの最大曲げ応力を正方形断面はりの1/2」との条件より、
⇒M×12/bh³×h/2 = M×12/a⁴×a/2×1/2 ⇒M×12/a²h²×h/2 = M×12/a⁴×a/2×1/2 ⇒ h=2a
⇒bh=a² ⇒ b×2a=a² ⇒ b=a/2


